光的衍射
衍射是定义光波与颗粒相互作用现象的术语。在这篇文章中,我们从衍射示例到光衍射方程阐述光波的衍射。
什么是衍射?
我们通常认为光总是沿直线传播,但当光波通过障碍物附近时,它们往往会绕过障碍物并扩散开来。衍射的定义是光波在通过或绕过障碍物时的扩散。更具体地说,如果作用于光,当光波经过边角或通过物理尺寸上近似于乃至小于该光波长的开口或狭缝时,就会发生光的衍射。
衍射示例
可以通过一种非常简单的方法来示范说明光波的衍射:将您的手放在光源前,然后慢慢并拢两个手指,同时观察从指缝间透射的光。当手指彼此靠近且几乎完全并拢时,您会开始看到一些平行于手指的暗线。这些平行线实际上是衍射图案。当光在与光的波长处于同一量级的颗粒周围“弯曲”时,也会发生这种现象。有一个例子可以充分说明这一点,即我们俗称为镶银边的云层对阳光的衍射这方面的一个很好的例子是太阳光被云层衍射,我们通常称之为“银线”,如图1所示海上美丽的日落。
我们经常可以看到云层呈现出淡淡的蓝色、粉红色、紫色和绿色,这些是当光从云中的水滴衍射时产生的现象。衍射量取决于光的波长,较短波长比较长波长的衍射角度更大(实际上现实中,蓝光和紫光的衍射角度大于红光)。当穿过大气层的光波遇到水滴时,如图2所示,它首先在空气-水界面发生折射,然后在再次遇到该界面时发生反射。仍在水滴内部传播的光束在第三次遇到该界面时会再次发生折射。与该界面的这最后一次交互作用会将光折射回大气层中,但它也会衍射一部分光,如下图所示。这种部分衍射会引发一种称为塞里尼晕(也称为“草露宝光”效应)的现象,即观察者头部的阴影周围有明亮的光环。

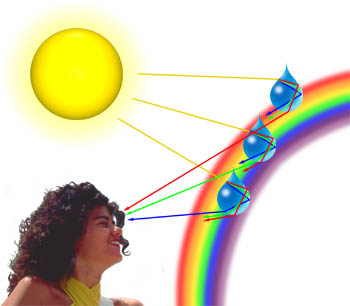
图2
衍射和散射有什么区别?
衍射和散射这两个术语通常可以互换使用,并且被认为几乎是同义词。衍射描述的是光散射的一种特例,即具有规则重复特征的对象(如衍射光栅)在衍射图案中产生有序的光衍射。在现实世界中,大多数对象的形状都非常复杂,应该被视为由许多单独的衍射特征组成,并且这些特征可以共同产生随机的光散射。
单缝光衍射实验
涉及光波衍射的经典和最基本的概念之一是单缝光衍射实验,该实验最早是在19世纪初进行的。当光波通过狭缝(或孔径)传播时,结果取决于孔径相对于入射光束波长的物理尺寸。图3说明了这一点,它假设从点光源S发射的相干单色波(类似于激光产生的光)通过孔径d并发生衍射,主入射光束落在P点,第一个次极大值出现在Q点。
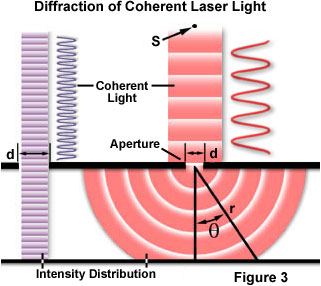
如图左侧所示,当波长(λ)远小于孔径宽度(d)时,光波继续沿直线传播,就像它是颗粒或不存在孔径一样。但当波长超过孔径的大小时,我们会根据以下方程经历光的衍射:
sinθ = λ/d
其中θ是入射中心传播方向与衍射图案第一个最小值之间的角度。该实验会产生一个明亮的中心最大值,其两侧是次极大值,每个后续次极大值的强度随着与中心距离的增加而减小。图4用光束强度与衍射半径关系图说明了这一点。请注意,出现在次极大值之间的极小值是π的倍数。
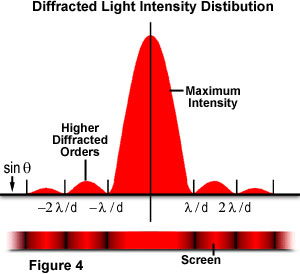
Augustin Fresnel首先对这个实验做出了解释,他与Thomas Young一起提供了证实光在波中传播的重要证据。从以上插图中,我们可以看到从L点发射的相干单色光(在本例中为激光照明)如何被孔径d衍射。Fresnel假设Q点处的一阶极大值的波幅(定义为εQ)将由以下公式得出:
dεQ = α(A/r)f(χ)d
其中A是入射波的波幅,r是d与Q之间的距离,f(χ)是χ的函数,后者是Fresnel引入的倾斜因子。
光的衍射在限制任何光学仪器(例如:照相机、双筒望远镜、望远镜、显微镜和眼睛)的分辨率方面起着至关重要的作用。分辨率是指光学仪器产生分辨两个相邻点的为单独图像的能力。这通常取决于仪器中镜头和反射镜的质量以及周围介质(通常是空气)的特性。光的波状性质导致所有光学仪器的分辨率都有一个极限。
圆形孔径衍射方程
我们对衍射的阐述使用了狭缝作为光衍射时通过的孔径。但所有光学仪器都具有圆形孔径,例如眼睛的瞳孔或显微镜的圆光阑和镜头。圆形孔径产生的衍射图案与上述类似,不同的是图案自然呈现圆形对称。以下衍射方程描述了由圆形孔径产生的衍射图案的数学分析方法:
sinθ(1) = 1.22(λ/d)
其中θ(1)是一阶衍射极小值(第一个暗环)的角位置,λ是入射光的波长,d是孔径的直径,1.22是常数。在大多数情况下,角度θ(1)非常小,因此角度的正弦和正切约略值几乎相等:
θ(1) ≅ 1.22(λ/d)
从这些方程中可以看出,中心最大值与λ/d成正比,这使得该最大值在波长较长和孔径较小时分散度更大。得益于这些镜头先天的光衍射,衍射的次极大值会限制光学显微镜中物镜镜头的有用放大倍率。无论镜头多么完美,镜头产生的点光源的图像都伴随有次极大值和更高阶的极大值。只有当镜头具有无限直径时,才能消除这种情况。距离小于θ(1)的两个对象无论放大倍率多高都无法分辨出来。虽然这些方程是针对距孔径无限远的点光源的图像推导出来的,但当用d代替物镜透镜的直径时,可以作为显微镜分辨率的合理约略值。
因此,如果两个对象彼此相距D并且与观察者的距离为L,则它们之间的角度(以弧度表示)为:
θ = D/L
这样我们就可以将最后两个方程简缩后得到以下方程:
D(0) = 1.22(λL/d)
其中D(0)是能够将对象分辨出来的对象之间最小分隔距离。使用这个衍射方程时,人眼可以分辨相距0.056毫米的对象,但视网膜中的光感受器靠得不够近,无法达到这种分辨率,在正常情况下,0.1毫米是更切合实际的数字。
光学显微镜的分辨率取决于许多因素,其中包括上面所阐述的因素,但在最理想的情况下,这个数字约为0.2微米。这个数字必须考虑显微镜的光学校直对准、镜头透镜的质量以及用于对标本成像的光的主波长。虽然通常没有必要计算每个物镜的准确分辨率(在大多数情况下会浪费时间),但了解显微镜镜头运用于现实世界时的能力非常重要。
对不起,此内容在您的国家不适用。